Min no of coins for change problem dynamic programming

Min no of coins for change dynamic programming problem

You are given an integer array coins representing coins of different denominations and an integer amount representing a total amount of money.

Return the fewest number of coins that you need to make up that amount. If that amount of money cannot be made up by any combination of the coins, return -1.

1. Why this is a dp problem - because we are asked to minimize the total number of coins for change, at each step/index we would be choosing minimum

2. There are 3 paths to take in this problem a. First path is arr[0] - amount (first dp call) b. Second path is arr[1] - amount (second dp call) c. Third path is arr[2] - amount (third dp call)

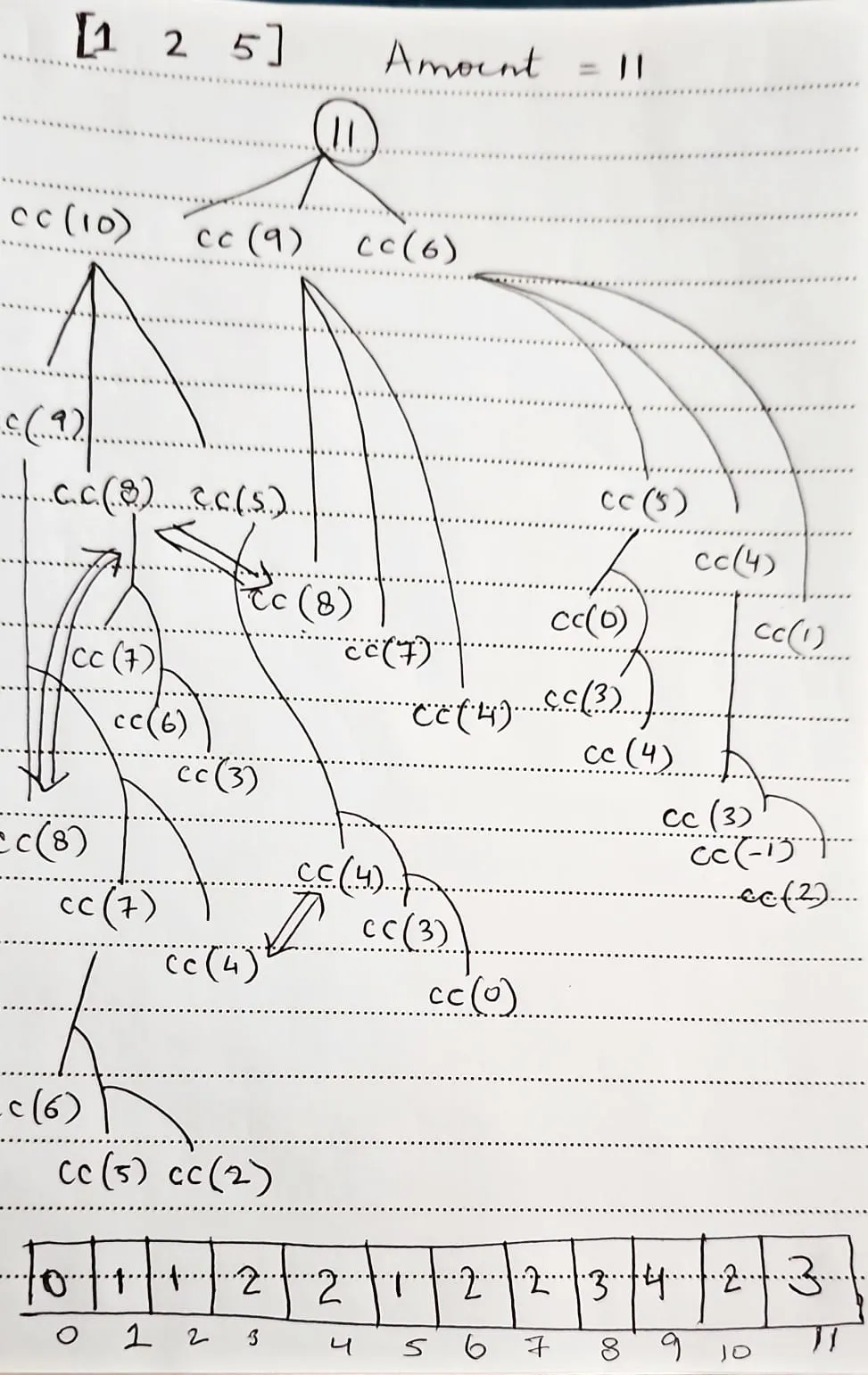
3. During recursion we would be able to fill the min coins needs to for each amount 1 to 11(example lets say toptal amount is 11)

4. Hand drawn diagram to explaining the recursion

    public static void main(String args[]) {
       CoinChange cc = new CoinChange();
       int[] arr = new int[]{1,2,5};
       int amount = 11;
       int[] dp = new int[amount];
       Arrays.fill(dp, -1);
       System.out.println(cc.coinChange(arr, amount, dp));
    }

    int coinCount = 0;
    
    private int coinChange(int[] coins, int remainingAmount, int dp[]) {
    if(remainingAmount < 0) {
        return -1;
    }
    if(remainingAmount == 0) {
        return 0;// there are 0 coins to make a sum zero
    }
    if(dp[remainingAmount-1] != -1){
        return dp[remainingAmount-1];
    }
    int min = Integer.MAX_VALUE; //done to have a global cal for result
    for (int coin : coins) {
       int coinCount = coinChange(coins, remainingAmount-coin, dp);
       if(coinCount >=0 && coinCount < min) {
         min = coinCount + 1;
       }
    }   
    dp[remainingAmount-1] = (min == Integer.MAX_VALUE) ? -1 : min; //updating the min amount in the array as well
    return min;
  }