Validate Binary Search Tree

Valid BST Given the root of a binary tree, determine if it is a valid binary search tree (BST). A valid BST is defined as follows:

The left subtree of a node contains only nodes with keys less than the node’s key. The right subtree of a node contains only nodes with keys greater than the node’s key. Both the left and right subtrees must also be binary search trees.

Both the subtrees would be said to be fulfilling the condition when:

1. Entire left subtree should be BST with right subtree
2. At any point of time right subtree should not be less than low and left subtree should not be more than high

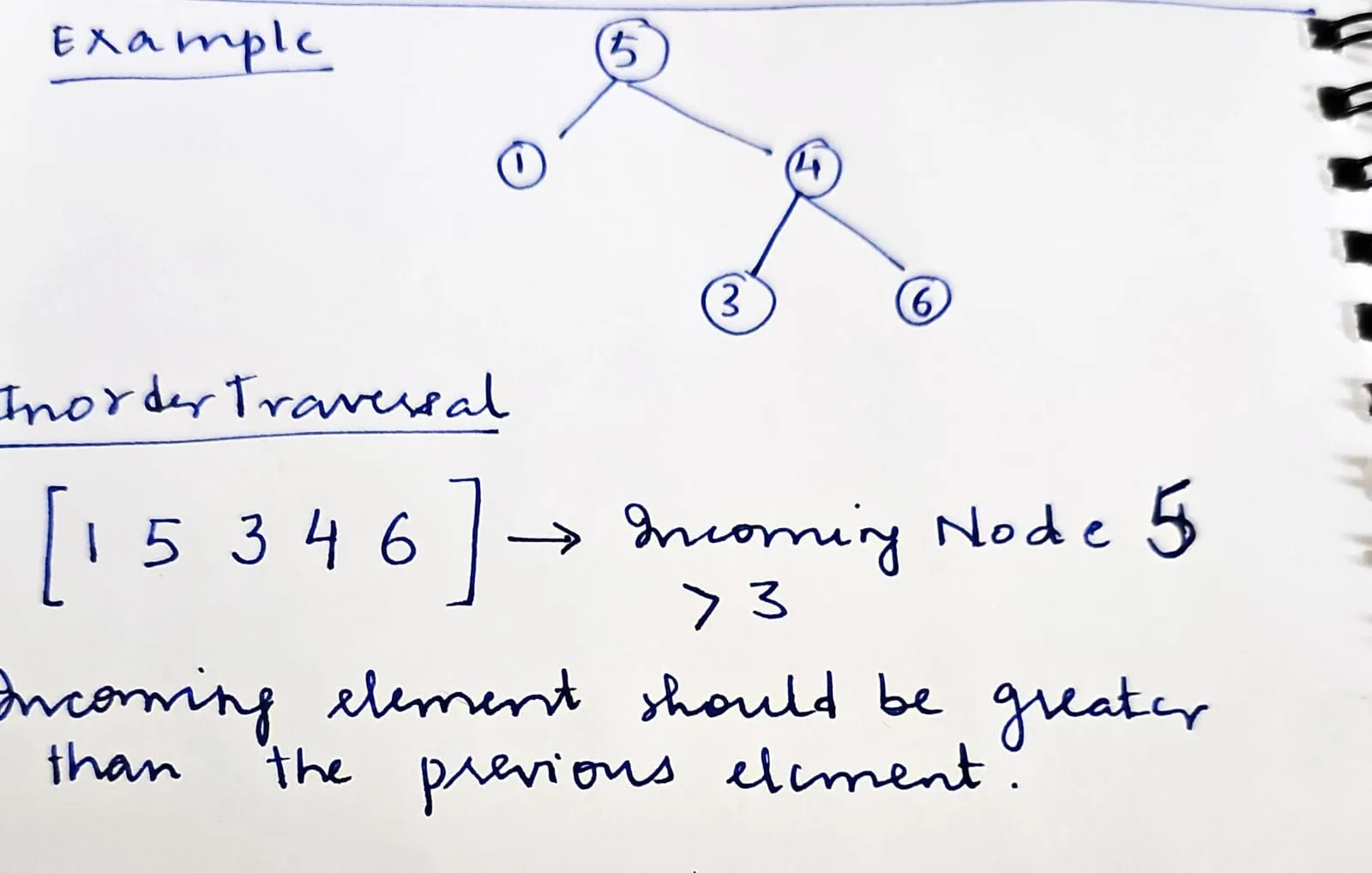
Alternative we can use inorder traversal, inorder traversal would return sorted order elements If in inorder traversal we have any incoming node smaller than the previous node we return false immediately

This is because in BST smaller elements are on the leftree and larger than root are on the right tree. Example [1, 2, 6, 4, 5] Here 6 > 4(root) hence it isnt a valid BST

 private boolean validBST(Node n, Node low, Node high) {
      if(n == null) {
         return true;
      }
      //binary search tree, the inorder travesal will be sorted
      if(low != null && n.val > low.val || high != null && n.val < high.val) {
        return false;
      }
      validBST(n.left, n, high);
      validBST(n.right, low, n);
      return true;
}
 private boolean inOrderTraversal(Node n, Node prev) {
        //Inorder traversal means LEFT, node , RIGHT
        if(n == null) {
            return false;
        }
        inOrderTraversal(n.left, prev);
        if(prev != null && n.val <= prev.val) {
            //inorder condition current node should nit be less than last node
            return false;
        }
        prev = n;
        inOrderTraversal(n.right, prev);

        return true;
}